| lvishd | 0 #421 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 28/11/2010 19:49
Post(s): 12664
Karma: 5543 |
Membre / date d'inscription / lieu / nourriture
poum / 2013 / topic a jeux / yahourt louxor / 2005 / sport / bonbons alex / 2014 / CDL / chien chaud stupe / 2012 / bar / kebab angel / 2004 / audio&visuel / frites 
Contribution le : 02/11/2014 13:29
|
|
 Signaler Signaler |
||
| -PAPI- | 0 #422 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 23/04/2013 21:46
Post(s): 5465
Karma: 403 |
@lvishd: c'est tout bon^^
Contribution le : 02/11/2014 14:10
|
|
 Signaler Signaler |
||
| lvishd | 0 #423 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 28/11/2010 19:49
Post(s): 12664
Karma: 5543 |
- Relance -
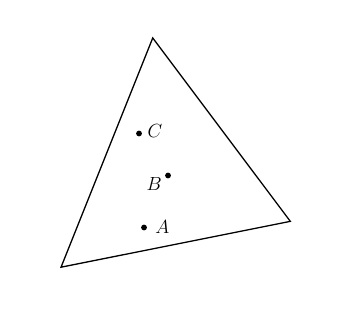 Quel est le centre de gravité? Justifier
Contribution le : 02/11/2014 14:46
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #424 |
|
|---|---|---|
|
J'aime glander ici
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
Si c'est v c'est vraiment tout pourri

Contribution le : 02/11/2014 16:02
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| lvishd | 0 #425 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 28/11/2010 19:49
Post(s): 12664
Karma: 5543 |
Citation :
 @toi
Contribution le : 02/11/2014 17:12
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #426 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
Roh mais non je voulais pas te vexer, j'y croyais même pas :-s
J'ai pas de relance du coup..
Contribution le : 02/11/2014 17:21
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| Invité | 0 #427 |
|
|---|---|---|
|
FantômeInvité
|
[Compte supprimé]
Contribution le : 02/11/2014 17:27
|
|
 Signaler Signaler |
||
| -PAPI- | 0 #428 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 23/04/2013 21:46
Post(s): 5465
Karma: 403 |
ben euh nan... à vrai dire il n'y a personne dans les topics à sports XD
Contribution le : 02/11/2014 17:42
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #429 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
Okay j'ai trouvé une relance
Un type choisit deux nombres entre 2 et 999 (qui peuvent être les mêmes). Il va ensuite voir Sam et Pauline. A Sam, il murmure la somme de ces deux nombres, et à Pauline le produit des deux. Voici la conversation qui s'ensuit: Pauline: Je ne connais pas les deux nombres. Sam: J'en étais sûr. Pauline: Je les connais maintenant. Sam: Moi aussi. Quels étaient les 2 nombres ?
Contribution le : 02/11/2014 18:34
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| Invité | 0 #430 |
|
|---|---|---|
|
FantômeInvité
|
[Compte supprimé]
Contribution le : 02/11/2014 18:42
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #431 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
En s'y mettant à plusieurs on devrait y arriver

Contribution le : 02/11/2014 19:04
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| Poum45 | 0 #432 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 03/12/2007 23:03
Post(s): 59592
Karma: 4214 |
Citation :
La vache, elle a l'air complexe pour mon p'tit cerveau:-o 1) Le produit n'est pas unique. Exemple 12 qui peut être 3 x 4 ou 2 x 6 Bon, ça laisse de la marge jusqu'à 999  2) Euuuh, je ne sais pas par quel bout la prendre là 
Contribution le : 02/11/2014 19:47
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #433 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
Le raisonnement se base pas mal sur la décomposition en nombres premiers.
Bah déjà on peut exclure le fait que les deux nombres soient premiers. Sinon Pauline aurait déduit du premier coup. Ensuite, il faut que la somme soit décomposable d'au moins deux manières en deux nombres pas tous les deux premiers (je sais pas si je suis clair). Sinon il y aurait eu une chance que le cas que je viens de dire se produise et Sam n'aurait pas été aussi catégorique. Vous êtes OK avec ça ?
Contribution le : 02/11/2014 20:02
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| -PAPI- | 0 #434 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 23/04/2013 21:46
Post(s): 5465
Karma: 403 |
Citation :
j'avoue je n'ai pas clairement saisis à 100% En tout cas d'accord pour dire que si les 2 nombres sont entier alors Pauline 'aurais su puisqu'on peut décomposé les nombre en multiplication de nombres premier par exemple 44=2x2x11 Et comme ça on peut connaitre tous les diviseur de 44 Sinon,si Sam était sur que Pauline ne trouverais jamais toute seule c'est parce que dans toutes les combinaisons qu'il pouvais avoir, il n'y auais pas 2 nombres premier ensemble.du coup soit n le nombre donné à Sam, il ne faudrais pas que le réulstat de n-x soit un nombre premier quand x l'est. Par exemple: 44-3=41 3 est premier et 41 aussi. La je ne sais pas comment faire la liste des n que Sam aurais pu avoir. (de manière simple^^). Après peut être qu'il peut-être plus simple de trouvé la réponse en cherchant pourquoi Pauline trouve avec l'affirmation de Sam
Contribution le : 03/11/2014 12:19
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #435 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
Alors exemple: 10 c'est 2+8, 7+3, ou 6+4.
Sam envisage les trois possibilités, et se dit que si c'est 3+7 alors on aura dit 21 à Pauline, et elle aurait determiné ses nombres immédiatement. Pourtant Sam est SUR que Pauline ne peut pas savoir. Donc c'est pas 10. C'est pas mal parce que du coup on peut éliminer tous les nombres qui sont somme de deux nombres premiers. Alors maintenant attention ça va aller très vite: On suppose vrai la conjecture de Goldbach. Bim. (En vrai elle a été verifiée jusqu’à amplement plus que 999 donc ça passe) Cette conjecture elle est tout con, elle dit que tout entier pair peut s'écrire comme la somme de deux nombres premiers. Donc la somme est pas un entier pair. Breve de comptoir: Les deux nombres sont de parité différentes.
Contribution le : 03/11/2014 23:38
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| -PAPI- | 0 #436 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 23/04/2013 21:46
Post(s): 5465
Karma: 403 |
Je ne me rappelais plus de cette conjecture, en même temps je ne l'ai vu qu'en spé math il y a pfiou très longtemps^^
mais oui du coup les nombres sont différents puisque sinon le nombre mystère serais paire. Une bonne nuit de sommeil me permettra peut-être de trouvé la réponse^^
Contribution le : 04/11/2014 00:03
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #437 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
On est à deux assertions sur quatre et on a déjà éliminé la moitié de l'infinité des nombres.
On va y arriver.
Contribution le : 04/11/2014 04:15
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| -PAPI- | 0 #438 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 23/04/2013 21:46
Post(s): 5465
Karma: 403 |
Donc pour savoir les 2 nombre mystère pauline n'a besoin de savoir qu'une chose, que le nombre de Sam soit impair?
bon si le nombre de Sam est impaire , alors dans les 2 nombres mystère il y a un nombre pair et un impaire. Du coup Pauline a eu un nombre mystère dont sa multiplication décomposé donne un seul nombre impaire premier (Si il y en avais 2 elle n pourais pas deviné les 2 nombres) et il y a au moins deux 2 Du coup il nous reste plus qu'à trouvé comment Sam peut trouver les 2 nombres. EDIT:je viens de voir que je me suis trompé dans Du coup l'un des 2 nombre est dans cette liste et l'autre est un nombre premier impaire La liste se rétrécie^^
Contribution le : 04/11/2014 09:16
|
|
 Signaler Signaler |
||
| AnGel8 | 0 #439 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/06/2007 17:01
Post(s): 5934
|
On a déjà établi que les deux nombres pouvaient pas être tous les deux premiers.
Donc ça peut pas être 2, le deuxpuissancen.
Contribution le : 04/11/2014 12:06
|
|
|
_________________
A god with man hands. Je m'appelle chop money eh eh |
||
 Signaler Signaler |
||
| -PAPI- | 0 #440 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 23/04/2013 21:46
Post(s): 5465
Karma: 403 |
âh oui mince je l'ai ajouté sans faire gaffe j'edit du coup
Contribution le : 04/11/2014 12:18
|
|
 Signaler Signaler |
||
Le sujet est verrouillé









