Videos streaming images jeux et buzz
Connexion






Perdu le mot de passe ?

Inscrivez-vous maintenant !
Menu Principal
Communauté



Pearusdoancaia
Faire une perpendiculaire d'une ligne passant par un point. C# Windows Form
 1  #1
Je viens d'arriver
Inscrit: 05/07/2019 18:39
Post(s): 68
Yo !

Voici ce que j'ai :

Citation :

Point T1P1 = new Point(100, 100);
Point T1P2 = new Point(400, 400);

Pen DePi = new Pen(Color.DeepPink, 1);

Bitmap DrawArea = new Bitmap(picky.Size.Width, picky.Size.Height);
Graphics g = Graphics.FromImage(DrawArea);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;

g.DrawLine(DePi, T1P1, T1P2);

picky.Image = DrawArea;


Voici sa représentation dans Geogebra :

ipfs QmTTkABKvXTmJaPBZ2LYTTtaPjeyrw4qPUHv8Qqh24z7Eg

Et voici ce que je veux :

ipfs Qma4kTfza1oQZHxHiFiR96eG9GhKfpAiazCW2hdEjcXVmC

Une perpendiculaire de la droite AB passant par le point A et faisant 50 cm.

Problème :
Je n'ai pas trouvé de méthodes permettant de faire des perpendiculaires.

Alors j'ai un peu révisé ma géométrie et mes maths et, dans un repère orthonormé, l'équation d'une droite c'est :

y = mx + h

y étant l'odonné d'un point sur la droite
x l'abscisse de ce même point
m la pante de la droite
h l'ordonné à l'origine

Voici, alors, ce que j'ai suivis pour essayer de faire une perpendiculaire sans de méthode toute faite :

https://www.youtube.com/watch?v=B9p3sVGypU4 (pour connaitre l'équation d'une droite perpendiculaire à une autre droite)

https://www.youtube.com/watch?v=jzbNANey-58 (pour savoir comment trouver m)

J'ai réussi à faire une perpendiculaire avec quelques calculs, mais actuellement je tombe sur un autre problème...

Bref, tout ça pour demander s'il existe une méthode pour directement faire une perpendiculaire d'une ligne par rapport à un point de la ligne ? Pour savoir si je me casse pas la tête pour rien à résoudre mes problèmes. Merci !

Contribution le : 21/04/2020 17:48
Signaler

wackybacky
Re: Faire une perpendiculaire d'une ligne passant par un point. C# Windows Form
 0  #2
Je viens d'arriver
Inscrit: 08/03/2009 21:57
Post(s): 12
Salut,

Importe la référence :

Citation :
System.Numerics


Puis utilise la classe Vector2:

Citation :

var a = new PointF(100, 100);
var b = new PointF(400, 400);
var c = new PointF(120, 300);

var pink = new Pen(Color.DeepPink, 1);
var turq = new Pen(Color.DarkTurquoise, 1);
var blue = new Pen(Color.DeepSkyBlue, 2);

var bmp = new Bitmap(Size.Width, Size.Height);
var g = Graphics.FromImage(bmp);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;

g.DrawLine(pink, a, b);

var va = new Vector2(a.X, a.Y);
var vb = new Vector2(b.X, b.Y);
var vc = new Vector2(c.X, c.Y);

var dir = Vector2.Normalize(vb - va);
var dot = Vector2.Dot(vc - va, dir);
var vd = va + dir * dot;

var d = new PointF(vd.X, vd.Y);

g.DrawLine(turq, c, d);

g.DrawRectangle(blue, a.X - 1f, a.Y - 1f, 2f, 2f);
g.DrawRectangle(blue, b.X - 1f, b.Y - 1f, 2f, 2f);
g.DrawRectangle(blue, c.X - 1f, c.Y - 1f, 2f, 2f);
g.DrawRectangle(blue, d.X - 1f, d.Y - 1f, 2f, 2f);

BackgroundImage = bmp;
BackgroundImageLayout = ImageLayout.None;


Résultat: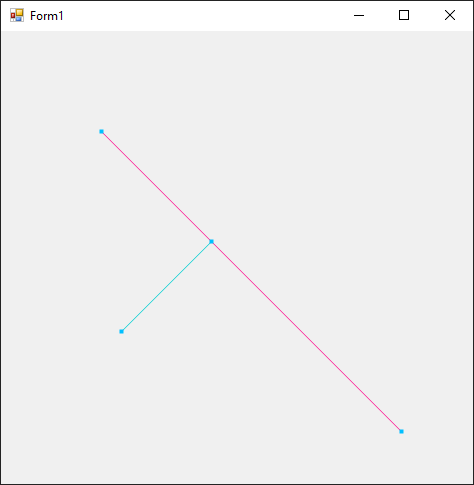



Edit: Possible hors sujet du au titre qui porte à confusion

Citation :
Faire une perpendiculaire d'une ligne passant par un point


La méthode ci-dessus décrit la façon de créer la perpendiculaire à une ligne passant par un point.

Contribution le : 25/04/2020 14:02
Signaler

wackybacky
Re: Faire une perpendiculaire d'une ligne passant par un point. C# Windows Form
 0  #3
Je viens d'arriver
Inscrit: 08/03/2009 21:57
Post(s): 12
Toujours avec la référence :

Citation :
System.Numerics


Citation :

var a = new PointF(100, 100);
var b = new PointF(400, 400);

var pink = new Pen(Color.DeepPink, 1);
var turq = new Pen(Color.DarkTurquoise, 1);
var blue = new Pen(Color.DeepSkyBlue, 2);

var bmp = new Bitmap(Size.Width, Size.Height);
var g = Graphics.FromImage(bmp);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;

g.DrawLine(pink, a, b);

var va = new Vector2(a.X, a.Y);
var vb = new Vector2(b.X, b.Y);

var cross = Vector3.Cross(Vector3.UnitZ, new Vector3(vb - va, 0)); // sens horaire, inverser pour tourner dans le sens trigo
var dir = Vector2.Normalize(new Vector2(cross.X, cross.Y));
var vc = va + dir * 50; // distance

var c = new PointF(vc.X, vc.Y);

g.DrawLine(turq, c, a);

g.DrawRectangle(blue, a.X - 1f, a.Y - 1f, 2f, 2f);
g.DrawRectangle(blue, b.X - 1f, b.Y - 1f, 2f, 2f);
g.DrawRectangle(blue, c.X - 1f, c.Y - 1f, 2f, 2f);

BackgroundImage = bmp;
BackgroundImageLayout = ImageLayout.None;


Résultat: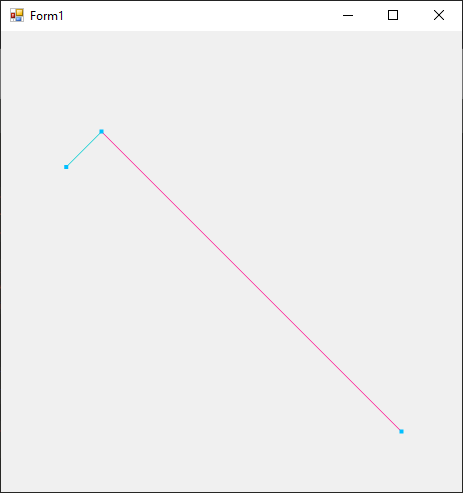


Contribution le : 25/04/2020 19:35
Signaler

Pearusdoancaia
Re: Faire une perpendiculaire d'une ligne passant par un point. C# Windows Form
 0  #4
Je viens d'arriver
Inscrit: 05/07/2019 18:39
Post(s): 68
@wackybacky Re, je reviens sur ce problème après quelque mois où je l'ai laissé de côté. Est-ce que tu pourrais détailler les calculs et ce que tu fais ?

Après réflexion je vais partager ce que je veux faire au final :

Lien Geogebra : https://www.geogebra.org/geometry/pr3z4cs7

Alors voilà, j'ai 2 droites AB et AC, dont les coordonnées des points, dans mon programme, sont : A(100;100) B(400;400) C(100;700)
Il faut que je fasse les parallèles de AB et de AC d'un espacement de 50 cm. Alors je trace ma perpendiculaire BE de 50 cm de la droite AB en passant par B, je fais la parallèle de AB passant par E puis je fais le même procédé pour la parallèle de AC : je trace ma perpendiculaire CD de 50 cm de la droite AC en passant par C et je fais la parallèle de AC passant par D.
Finalement ça me donne le point F et je trace le cercle de centre F et de rayon 50 cm.

Je me suis basé sur cette vidéo : https://www.youtube.com/watch?v=h-KBRwkdtKs

En sachant que visuellement, il ne doit apparaître que ce qui est en rose, comment je reproduis tout ça en C# ?

Contribution le : 24/07/2020 14:09
Signaler

wackybacky
Re: Faire une perpendiculaire d'une ligne passant par un point. C# Windows Form
 0  #5
Je viens d'arriver
Inscrit: 08/03/2009 21:57
Post(s): 12
Voici une version simplifiée:
https://www.geogebra.org/geometry/mtxfwdvj

Entrée:
Soit A, B, C trois points du plan, f le segment [AB] et g le segment [BC]. Soit r le rayon de cintrage.

Sortie:
Soit D le centre de l'arc de cintrage, E et F les points de tangence entre l'arc de cintrage et les segments f et g.

D = Point(B, Vecteur(r / sin(Angle(A, B, C) / 2) VecteurUnitaire(VecteurUnitaire(Vecteur(B, A)) + VecteurUnitaire(Vecteur(B, C)))))
Le décalage du point B dans la direction du vecteur somme |BA| + |BC| (normalisés) à une distance de r / sin(Angle(A, B, C) / 2

E = Point(B, Vecteur(r / tan(Angle(A, B, C) / 2) VecteurUnitaire(Vecteur(B, A))))
Le décalage du point B dans la direction du vecteur BA à une distance de r / tan(Angle(A, B, C) / 2)

F = Point(B, Vecteur(r / tan(Angle(A, B, C) / 2) VecteurUnitaire(Vecteur(B, C))))
Le décalage du point B dans la direction du vecteur BC à une distance de r / tan(Angle(A, B, C) / 2)

Explore la classe System.Numerics.Vector2, tu trouvera tout ce qu'il te faut pour réaliser ton programme.

Bonne chance.

Contribution le : 03/09/2020 23:42
Signaler

wackybacky
Re: Faire une perpendiculaire d'une ligne passant par un point. C# Windows Form
 0  #6
Je viens d'arriver
Inscrit: 08/03/2009 21:57
Post(s): 12
Compile, teste et analyse ce projet: BendingDemo
Tu trouvera le code source dans le fichier DemoForm.cs

Contribution le : 04/09/2020 01:52
Signaler


 Haut   Précédent   Suivant






Suivez Koreus sur : ▶︎ Mastodon ▶︎ Twitter ▶︎ Telegram ▶︎ Dailymotion | Flux RSS | Koreus Network | Archives

Si vous êtes l'auteur d'un élément de ce site, vous pouvez si vous le souhaitez, le modifier ou le supprimer
Merci de me contacter par mail. Déclaré à la CNIL N°1031721.