| CrazyCow | [Mathématiques] Nombres parfaits |
3 #1 |
|---|---|---|
|
Je poste trop
 
Inscrit: 29/07/2008 00:26
Post(s): 18991
Karma: 29871 |
Hello,
Si j'ai bien compris aujourd'hui on ne connaîtrait que 50 nombres parfaits. J'ai voulu m'amuser en codant un programme permettant de vérifier si un nombre est parfait, sans m'intéresser au préalable aux études faites sur le sujet. Après avoir trouvé les 4 premiers j'ai essayé de trouver une logique, s'il y en avait une. Comme j'ai vu que ces 4 premiers nombres étaient proches de puissances de 2, j'en ai déduis la formule suivante : y = 2^(2x+1) - 2^x Via mon programme j'ai testé directement tous les y que me donne la formule en incrémentant x de 1 à chaque fois. Et cette formule s'est révélée juste sur tous les calculs que j'ai fait, jusqu'à ce que la mémoire soit saturée (au 17ème nombre parfait). Ensuite j'ai regardé un peu plus en détail sur Internet, mais je n'ai retrouvé cette formule nul part. C'est la formule d'Euclide, qui utilise des nombres premiers de Mersenne, qui est mise en avant (d'où la limitation actuelle à 50 nombres) : Explications de cette formule Est-ce que je me suis trompé quelque part ? 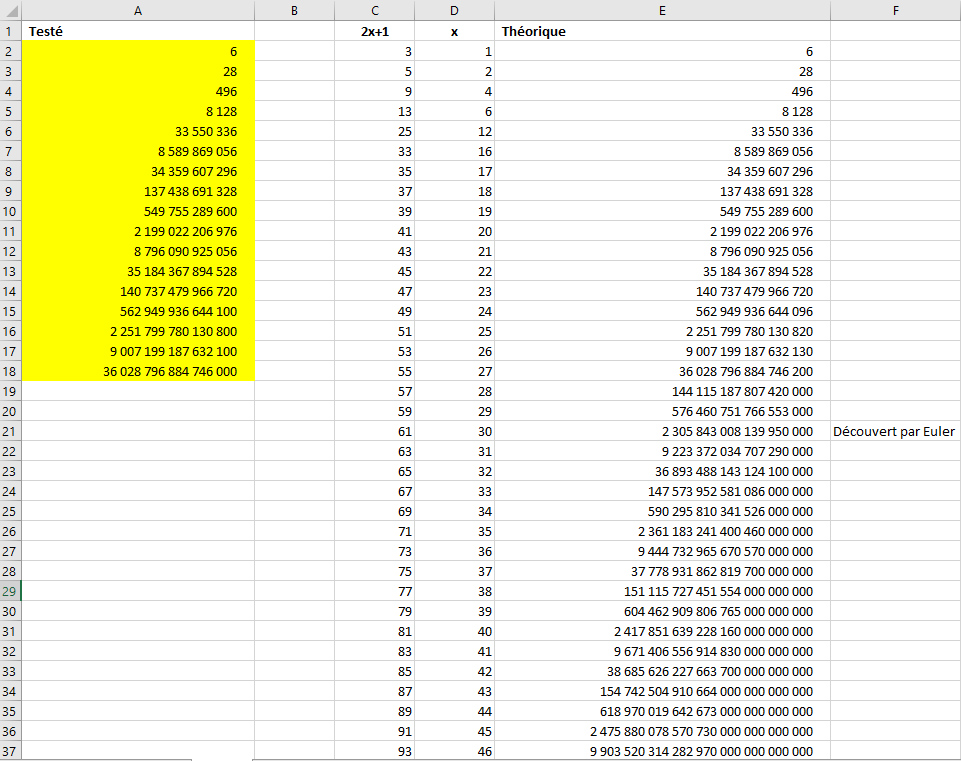 (Quand x n'est pas marqué, c'est que le résultat n'est pas un nombre parfait)
Contribution le : 08/08/2018 14:04
|
|
|
_________________
  K TROPHY K TROPHY “ À un moment donné, il faut lâcher prise. Claude François |
||
 Signaler Signaler |
||
| aioren | 0 #2 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 07/09/2004 22:27
Post(s): 14002
Karma: 3937 |
Ils ont une utilité particulières ces nombres ou c'est juste pour la beauté de l'art ?
Des bisous 
Contribution le : 08/08/2018 17:06
|
|
|
_________________
AWARD NATIONALE 2015 : Klaxon |
||
 Signaler Signaler |
||
| CrazyCow | 0 #3 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 29/07/2008 00:26
Post(s): 18991
Karma: 29871 |
@aioren Non ils ne servent à rien je crois. Les Grecs dans leur numérologie nommaient les nombres en fonction de leur "beauté". Il y a donc les nombres parfaits, mais il y a aussi les nombres "déficients", "abondants", "pratiques". Des couples de nombres ayant une relation entre eux au niveau de leurs diviseurs peuvent être "amical", "sociable"

Contribution le : 08/08/2018 17:28
|
|
|
_________________
  K TROPHY K TROPHY “ À un moment donné, il faut lâcher prise. Claude François |
||
 Signaler Signaler |
||
| Mitri | 0 #4 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 14/12/2006 19:51
Post(s): 10037
Karma: 1123 |
@CrazyCow Oui tu t’es planté et non, ta formule n’est pas bonne pour x = 0
Il y a donc un point qui cloche
Contribution le : 08/08/2018 18:31
|
|
|
_________________
Light is broken inside, but i still work |
||
 Signaler Signaler |
||
| Baba-Yaga | 2 #5 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 10/07/2016 18:17
Post(s): 18941
Karma: 13129 |
@CrazyCow
Ton calcul peut-il servir à améliorer nos couvaisons ?
Contribution le : 08/08/2018 19:49
|
|
|
_________________
M'en fous, j'ai gagné ! |
||
 Signaler Signaler |
||
| jopopmk | 2 #6 |
|
|---|---|---|
|
Je m'installe
 
Inscrit: 26/11/2013 20:17
Post(s): 388
Karma: 700 |
La formule d'Euclide n'est pas pour un p quelconque dans l'ensemble des entiers, mais pour p vérifiant que :
- p est un nombre premier, - 2^p -1 est un nombre premier. Si tu reprends la formule d'Euclide, que tu poses p=x+1 et que tu développes, tu devrais retomber sur ta formule perso 
Contribution le : 09/08/2018 11:32
|
|
 Signaler Signaler |
||
| CrazyCow | 1 #7 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 29/07/2008 00:26
Post(s): 18991
Karma: 29871 |
Merci pour vos réponses.
Je vois que la fonction que j'ai utilisé (elle n'est pas de moi) pour trouver les diviseurs ne fonctionne pas comme il faut pour les grands nombres. C'est à mon avis la raison principale qui explique que mon programme détectait des nombres parfaits qui n'en sont pas comme 549 755 289 600 par exemple. Une fois le programme corrigé on devrait pouvoir s'en servir pour couver.
Contribution le : 09/08/2018 13:20
|
|
|
_________________
  K TROPHY K TROPHY “ À un moment donné, il faut lâcher prise. Claude François |
||
 Signaler Signaler |
||






