| Anthooo | Enigmes - Volume XVII |
1 #1 |
|---|---|---|
|
J'aime glander ici
 
Inscrit: 20/05/2016 19:01
Post(s): 6543
Karma: 3348 |
Règles:
• Il est strictement interdit de s'aider du web pour trouver la solution d'une énigme, à part si elle fait appelle à des notions de culture. Dans ce cas, et uniquement dans ce cas, la recherche doit être effectuée pour comprendre l'énigme et non la résoudre. • Une personne qui trouve la solution doit détailler sa réponse si l'énigme fait appel à un raisonnement complexe. Ca peut être un dessin, une démonstration ... etc • Si la personne relance avec une énigme déjà passée, signalez par écrit le lien du post du DJP. Dans ce cas, la personne doit relancer avec une autre énigme. • Si au bout de 1 journée l'énigme n'est pas résolue, vous êtes en droit de mentionner le posteur de l'énigme pour lui demander un indice. • Si au bout de 3 jours l'énigme n'est pas résolue, vous êtes en droit de mentionner le posteur de l'énigme pour lui demander la solution. • Si 24h après la mention du posteur pour obtenir la solution, ce dernier n'a pas répondu, vous êtes en droit de relancer une nouvelle énigme, en ignorant la précédente. - Il est fortement conseillé de reformuler les énigmes si vous allez les chercher sur des sites web, en changeant à la fois le vocabulaire et les tournures de phrase, quitte à partir dans un sketch en réutilisant des pseudos de Koreusiens. - Si vous tentez de créer une énigme. Testez là d'abord sur votre entourage. La solution doit se trouver facilement par la logique et la solution ne doit pas être abracadabrante. Exemple de ce que nous ne voulons pas: "complétez la suite: R-D-T-D ? solution : E car Règles Du Topic Des Enigmes. Si vous n'arrivez pas à interprêter le règlement dans votre situation, vous DEVEZ prévenir un modérateur de la Section (Zertyy ou Wiliwilliam_) Les modérateurs sont en droit de ne pas respecter les règles (notamment celle des délais d'attente) pour assurer le bon fonctionnement et la conservation d'un bon rythme du topic des Enigmes Bon jeu à tous! Les topics précédents : Volume XVI Volume XV Volume XIV Volume XIII Volume XII Volume XI Volume X Volume IX Volume VIII Volume VII Volume VI Volume V Volume IV Volume III Volume II Volume I La relance est à Nyark_Nyark
Contribution le : 22/10/2016 17:50
Edité par Anthooo sur 7/11/2016 22:06:50
|
|
|
_________________
 |
||
 Signaler Signaler |
||
| Nyark_Nyark | 0 #2 |
|
|---|---|---|
|
Je masterise !
 
Inscrit: 29/01/2015 14:41
Post(s): 2909
Karma: 1830 |
Je vous emmène au ski pour la relance.
On va devoir prendre le télésiège pour se rendre en haut des pistes. Les sièges de ce télésiège sont numérotés à partir de 1 (1, 2, 3, 4, etc...). Quand le siège 15 croise le siège 27, le siège 56 croise le siège 118. Combien y a-t-il de sièges au total ?
Contribution le : 23/10/2016 17:32
|
|
 Signaler Signaler |
||
| Wiliwilliam | 0 #3 |
|
|---|---|---|
|
La loi c'est moi
 
Inscrit: 07/04/2012 19:19
Post(s): 38225
Karma: 18959 |
118+15=132?
'faut s'imaginer deux lignes avec les sièges devant et les sièges derrières.
Contribution le : 23/10/2016 18:08
|
|
|
_________________
>> Récompenses si tu passes en article << |
||
 Signaler Signaler |
||
| Anthooo | 0 #4 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 20/05/2016 19:01
Post(s): 6543
Karma: 3348 |
Devancé par @Wiliwilliam_ ça fait depuis 30 minutes que je planche dessus
 Parfois je me complique la vie alors que c'était aussi simple que ça. Je vous explique quand même mon raisonnement: 1/ J'ai représenté l'appareil dans un tableau (dans ce cas la montée se fait à droite, ici on voit le moment ou le 27 croise le 15 2/ J'ai ensuite tiré mes colonnes pour arriver au moment où le 56 croise le 118 Ensuite il me restait plus qu’à tirer ma colonne de droite pour avoir le nombre exact de siège. Au moins on a la preuve par le graphique + par le calcul  C'est un truc que j'arrive jamais à comprendre ces croisements de sièges, heureusement au boulot j'ai un tableau de correspondance un peu similaire à ce que j'ai représenté ^^
Contribution le : 23/10/2016 18:16
|
|
|
_________________
 |
||
 Signaler Signaler |
||
| Nyark_Nyark | 0 #5 |
|
|---|---|---|
|
Je masterise !
 
Inscrit: 29/01/2015 14:41
Post(s): 2909
Karma: 1830 |
@Wiliwilliam_ Attends, attends, attends...
J'ai pas bien compris ton raisonnement. Si par exemple l'avais dit : Quand le siège 13 croise le siège 25, le siège 46 croise le siège 112. Qu'est ce que tu m'aurais proposé ?
Contribution le : 23/10/2016 18:27
|
|
 Signaler Signaler |
||
| Wiliwilliam | 0 #6 |
|
|---|---|---|
|
La loi c'est moi
 
Inscrit: 07/04/2012 19:19
Post(s): 38225
Karma: 18959 |
@Nyark_Nyark
ok ok je détaille  27+15=42 ça c'est la valeur à laquelle on croise le siège le plus éloigné. or tu dis qu'on croise le 118 avec le 56 donc 118 + (56-42) = 132 (j'avoue avoir voulu vous enfumer avec mon 118+15 (-1) :lol:) dans ton second exemple ça aurait été 120 la réponse 112+[46-(25+13)] Satisfait? :lol:
Contribution le : 23/10/2016 18:36
|
|
|
_________________
>> Récompenses si tu passes en article << |
||
 Signaler Signaler |
||
| Nyark_Nyark | 0 #7 |
|
|---|---|---|
|
Je masterise !
 
Inscrit: 29/01/2015 14:41
Post(s): 2909
Karma: 1830 |
@Wiliwilliam_ Alors comme ça, d'accord. ^^

Contribution le : 23/10/2016 18:48
|
|
 Signaler Signaler |
||
| Wiliwilliam | 0 #8 |
|
|---|---|---|
|
La loi c'est moi
 
Inscrit: 07/04/2012 19:19
Post(s): 38225
Karma: 18959 |
Énoncé:
chaque colonne = 65 chaque ligne = 65 Les diagonales = 65 il faut utiliser tous les nombres de 1 à 25. 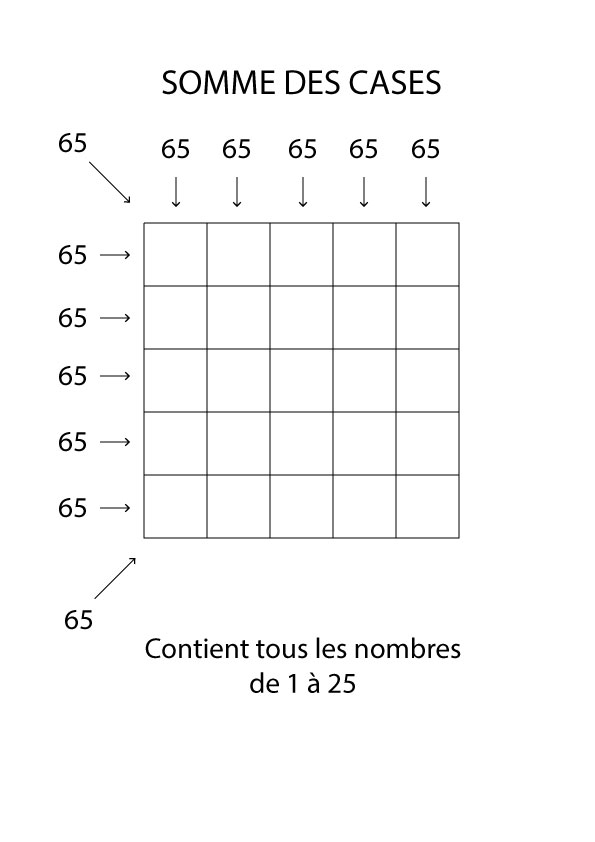 indice: 'y a une technique pour le remplir en 15s montre en main.
Contribution le : 23/10/2016 18:51
|
|
|
_________________
>> Récompenses si tu passes en article << |
||
 Signaler Signaler |
||
| Insert | 0 #9 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/07/2010 18:11
Post(s): 7720
Karma: 2193 |
J'imagine qu'il faut un 13 au centre, et ensuite, on ajoute des nombres qui font 52.
Donc on pourrait placer des blocs de 2 nombres qui feraient 26. Avec 2 blocs-qui-font-26 sur une même ligne, colonne, diag, on fait 52 et avec le centre, on fait 65. Reste à trouver comment les placer pour que les zones intermédiaires fassent aussi 65... Un histoire de symétrie j'imagine, mais ça ne me vient pas :gratte:
Contribution le : 23/10/2016 19:44
|
|
 Signaler Signaler |
||
| Insert | 0 #10 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/07/2010 18:11
Post(s): 7720
Karma: 2193 |
@Wiliwilliam_
Après des calculs, une résolution par pivot de Gauss, un tableur et du tatonnement, je trouve Mais je vois pas du tout comment le trouver "facilement" :gratte:
Contribution le : 26/10/2016 00:50
|
|
 Signaler Signaler |
||
| Poum45 | 0 #11 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 03/12/2007 23:03
Post(s): 59592
Karma: 4214 |
Citation :
C'est ultra simple. Faut commencer au centre de la première ligne. Tu montes toujours en diagonale (haut-droite). - Si tu sors à droite, tu reviens à gauche de la ligne. - Si tu sors en haut, faudra descendre en bas de la colonne. - Si tu es bloqué, tu descends d'une case. Avec cette méthode, tu rempli tous les carrés magiques impaires.
Contribution le : 26/10/2016 00:59
|
|
 Signaler Signaler |
||
| Insert | 0 #12 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/07/2010 18:11
Post(s): 7720
Karma: 2193 |
@Poum45
 Ok j'aurais jamais trouvé ça comme ça, par hasard ^^ Ok j'aurais jamais trouvé ça comme ça, par hasard ^^Ben je te laisse relancer du coup ?
Contribution le : 26/10/2016 01:08
|
|
 Signaler Signaler |
||
| Poum45 | 0 #13 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 03/12/2007 23:03
Post(s): 59592
Karma: 4214 |
@Insert du tout, à toi la relance
 Pour info, il y a une autre méthode pour les carrés paires mais aussi des trucs de malade, que je ne connais pas, qui sont utilisés par des magiciens.
Contribution le : 26/10/2016 01:09
|
|
 Signaler Signaler |
||
| Insert | 0 #14 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/07/2010 18:11
Post(s): 7720
Karma: 2193 |
À moins que @Wiliwilliam_ ait une objection, je relance ?
relance : Voici un très joli graphe On y trouve des sommets, reliés ou non par des arêtes. Mais ce n'est pas un graphe planaire. En effet, certaines de ces arêtes se coupent. Certains graphes peuvent être rendu planaire, voici un exemple : On peut déplacer les sommets, déplacer les arêtes, bref, redessiner les choses un peu comme on veut, mais il convient de garder le "même" graphe, c'est à dire qu'un sommet doit toujours être relié aux mêmes arêtes. En théorie des graphes, on aime les graphes planaires. C'est simple, c'est clair, on comprend bien les liens qu'ont les sommets entre eux. Seriez-vous capable de rendre planaire mon joli graphe ? Pour vous simplifier la vie, numérotez les sommets, vous pourrez ainsi vérifier que vous ne faites pas n'importe quoi. si dans mon dessin, le sommet 1 est relié au 5 et au 8, il doit, dans votre dessin final être relié... au 5 et au 8.
Contribution le : 26/10/2016 01:24
|
|
 Signaler Signaler |
||
| Poum45 | 0 #15 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 03/12/2007 23:03
Post(s): 59592
Karma: 4214 |
Je n'ai rien compris
 Même pas l'exemple :roll: Même pas l'exemple :roll:
Contribution le : 26/10/2016 02:46
|
|
 Signaler Signaler |
||
| Insert | 0 #16 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/07/2010 18:11
Post(s): 7720
Karma: 2193 |
Citation :
Sérieux ? ^^ Bon, je la refais : 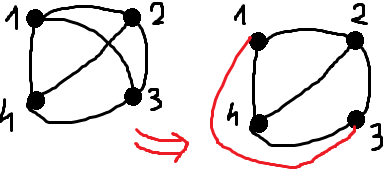 Dans mon premier dessin, les sommets : -1 est relié au 2, 3, 4, -2 est relié au 1, 3, 4, -3 est relié au 1, 2, 4, -4 est relié au 1, 2, 3. On constate que l'arête (1,3) qui relie le sommet 1 et 3 traverse l'arête (2,4). Mais on peut trouver une autre façon de dessiner le graphe, en reliant toujours les sommets aux mêmes sommets qu'avant, mais sans qu'aucune arête n'en croise une autre. Si ça t'aide de voir les choses ainsi, chaque point est une maison, chaque trait un raccordement entre maisons et il faut pas que les raccordements se croisent ^^
Contribution le : 26/10/2016 10:14
|
|
 Signaler Signaler |
||
| Poum45 | 0 #17 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 03/12/2007 23:03
Post(s): 59592
Karma: 4214 |
@Insert Je ne devais pas être bien réveillé. Là OK, j'ai tout compris

Contribution le : 26/10/2016 16:33
|
|
 Signaler Signaler |
||
| Nyark_Nyark | 0 #18 |
|
|---|---|---|
|
Je masterise !
 
Inscrit: 29/01/2015 14:41
Post(s): 2909
Karma: 1830 |
Contribution le : 26/10/2016 17:16
|
|
 Signaler Signaler |
||
| Poum45 | 0 #19 |
|
|---|---|---|
|
Je poste trop
 
Inscrit: 03/12/2007 23:03
Post(s): 59592
Karma: 4214 |
@Nyark_Nyark je n'ai pas vérifié mais tu as bien bossé

Contribution le : 26/10/2016 20:37
|
|
 Signaler Signaler |
||
| Insert | 0 #20 |
|
|---|---|---|
|
J'aime glander ici
 
Inscrit: 06/07/2010 18:11
Post(s): 7720
Karma: 2193 |
En effet @Nyark_Nyark c'est juste, on pouvait aussi le voir ainsi :
@toi 
Contribution le : 26/10/2016 22:08
|
|
 Signaler Signaler |
||









